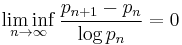Cem Yıldırım

Cem Yalçın Yıldırım (b. 8. July 1961)[1] is a Turkish mathematician who specializes in number theory. He obtained his PhD from the University of Toronto in 1990. His advisor was John Friedlander. He is currently a faculty member at Boğaziçi University in Istanbul, Turkey.

In 2005([2]), with Dan Goldston and János Pintz, he proved, that for any positive number ε there exist primes p and p′ such that the difference between p and p′ is smaller than ε log p.

Formally;

\liminf_{n\to\infty}\frac{p_{n%2B1}-p_n}{\log p_n}=0

where pn denotes the nth prime number. In other words, for every c>0, there exist infinitely many pairs of consecutive primes pn and pn+1 which are closer to each other than the average distance between consecutive primes by a factor of c, i.e., pn+1-pn<c log pn.

This result was originally reported in 2003 by Dan Goldston and Cem Yıldırım but was later retracted.[3][4] Then Janos Pintz joined the team and they completed the proof in 2005.

In fact, if they assume the Elliott-Halberstam conjecture, then they can also show that primes within 16 of each other occur infinitely often, which is related to the twin prime conjecture.

See also

References

  1. ^ VIAF
  2. ^ http://front.math.ucdavis.edu/math.NT/0508185
  3. ^ http://aimath.org/primegaps/
  4. ^ http://www.aimath.org/primegaps/residueerror/

External links